Objectives
- Understand how to use our knowledge of parametric equations to specify paths on a surface
- Use path limits as a means to find showing limits of multivariable functions do not exist
Section 6.4 Limits and Continuity of Multivariable Functions
At this point we have two versions of limits in our multivariable calculus class. For one, we have the limit of a vector valued function or parametric equation given by \(\mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle \text{.}\) These limits are expressed at the input \(t\) approaches a value and are essentially three single variable limits, similar to those you encountered in your first calculus course:
\begin{equation*}
\lim_{t \to c} \mathbf{r}(t) = \lim_{t\to c} \langle x(t), y(t), z(t) \rangle .
\end{equation*}
As usual, you have to consider \(t\) approaching \(c\) from the left and the right when computing the above limit.
We now also have the limit of a multivariable function \(f\) as \((x,y)\) approaches a point \((a,b)\)
\begin{equation*}
\lim_{(x,y) \to (a,b)} f(x,y) \text{.}
\end{equation*}
From our lessons, you have come to the conclusion that these are more complicated as there many directions (and paths) from which the point \((a,b)\) can be approached. These two limits have seen very different, but there is some connection between the two, which we explore in the examples and activities below.
Subsection 6.4.1 Paths on Multivariable Functions
Any two dimensional curve can be overlayed onto any surface. If you have a curve \(c(t)=(x(t), y(t))\) in two dimensions, then this can be overlayed onto a surface \(z=f(x,y)\) by substituting the values for \(x(t)\) and \(y(t)\) into the function \(f\text{.}\) This give us the parametric equation (or vector valued function) given by
\begin{equation}
\mathbf{r}(t) = \langle x(t), y(t), f(x(t), y(t)) \rangle \text{.}\tag{6.4.1}
\end{equation}
Example 6.4.2.
Consider the multivariable function given by
\begin{equation*}
f(x,y) = x^2-y^2
\end{equation*}
and the elliptical path in 2d given by
\begin{equation*}
x(t) = 2\cos(t) \qquad \text{and} \qquad y(t) = 3\sin(t)
\end{equation*}
with \(0 \leq t \leq 2\pi\text{.}\) As you may recall for Section 1.3 this path traverses an ellipse counter clockwise starting at \((2,0)\text{.}\) We can overlay this path on the function we can use (6.4.1). To this, end we get
\begin{align*}
\mathbf{r}(t) & = \langle x(t), y(t), f((x(t), y(t)) \rangle \\
& = \langle x(t), y(t), x(t)^2-y(t)^2 \rangle \\
& = \langle 2\cos(t), 3\sin(t), 4\cos^2(t)-9\sin^2(t) \rangle
\end{align*}
The path \(c(t) = (x(t), r(t))\) is display below in two dimensions along with the function \(f\) and the path \(\mathbf{r}\) in three dimensions.
Activity 6.4.1.
Let us try an example of creating several paths on a surface.
(a)
Consider the two dimensional paths given by
\begin{align*}
c_1(t) &= (2\cos(t), 2\sin(t)) & \qquad c_2(t)= (2-t, t^2-1) \qquad & c_3(t) = (1-2t, 2+t)\\
0 \leq &t \leq 2\pi & \qquad -2 \leq t \leq 2 \qquad & -3 \leq t \leq 3
\end{align*}
Graph \(c_1, c_2, c_3\) on a two dimensional plot. Use the Desmos tool below to confirm your results.
(b)
Now using the function
\begin{equation*}
f(x,y) = 2\cos(x+y)
\end{equation*}
Using (6.4.1) create paths on the surface of \(f\) given by \(\mathbf{r_1}, \mathbf{r_2}, \mathbf{r_3}\text{.}\)
(c)
Use the tool below to graph each path and verify that it corresponds to the \(c_1, c_2, c_3\) overlayed on the surface.
Subsection 6.4.2 Limits Multivariable Functions Not Existing
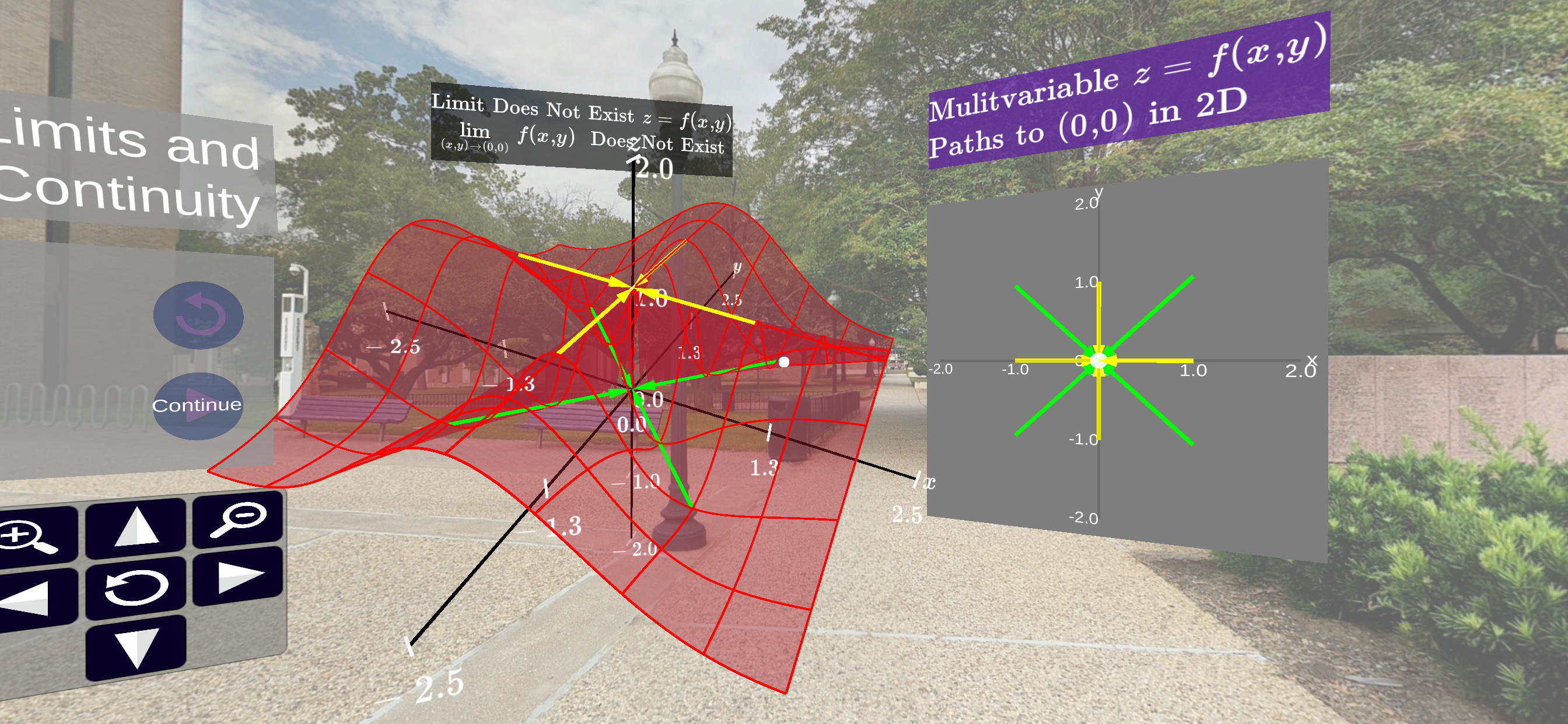
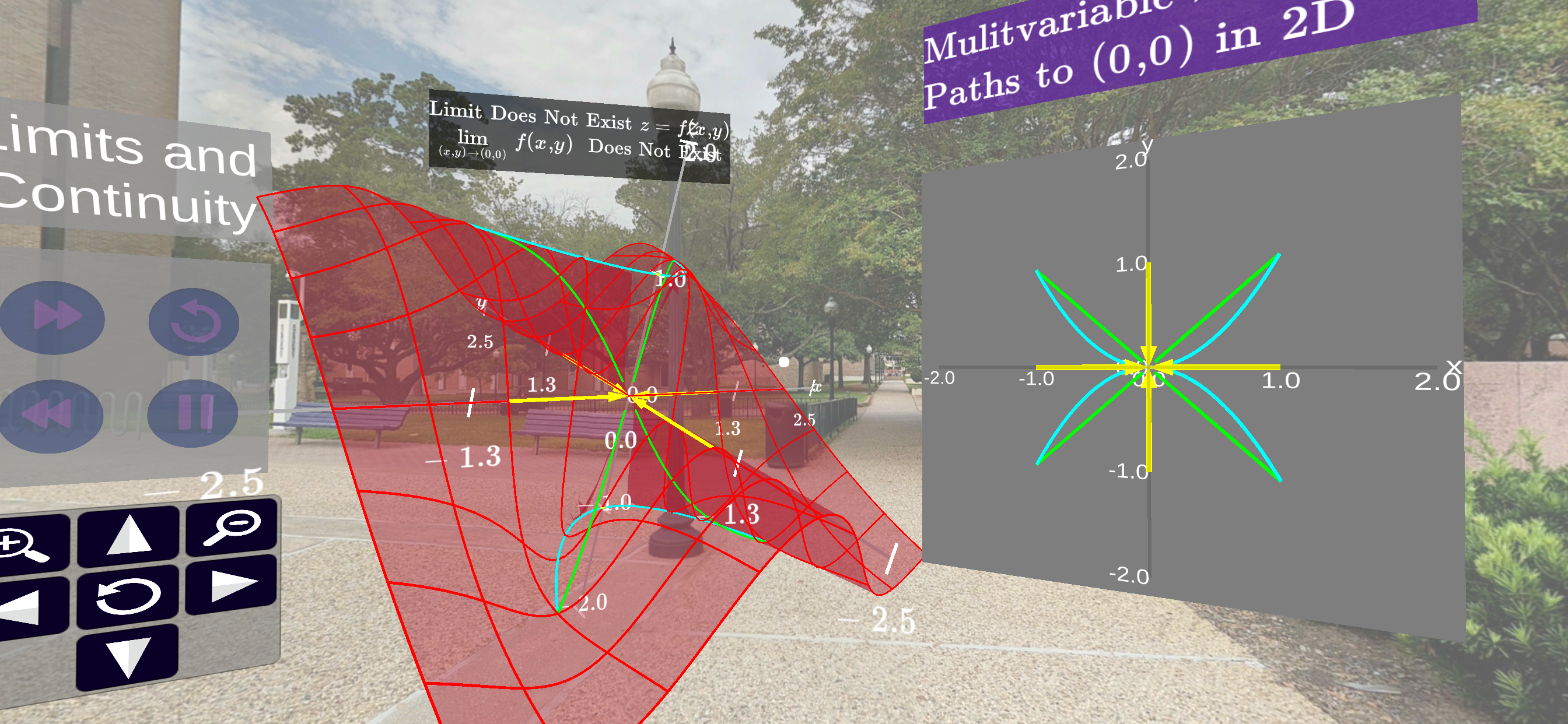
As we have seen in our lessons, it can be very difficult to determine if a limit such as
\begin{equation*}
\lim_{(x,y) \to (a,b)} f(x,y)
\end{equation*}
exists. However, to discover that such a limit does not exist, all that is required is to find two paths going to \((a,b)\) such that \(f(x,y)\) converges to different values as it follows these paths. Let’s introduce the notation of the previous section and expound on this notion. Suppose we have two paths \(c_1(t) = (x_1(t), y_1(t))\) and \(c_2(t)=(x_2(t), y_2(t))\) such that both
\begin{equation*}
\lim_{t \to t_0} c_1(t) = (a,b) \qquad \text{and} \qquad \lim_{t\to t_0} c_2(t) = (a,b)\text{.}
\end{equation*}
That is, both paths go to \((a,b)\) as \(t\to t_0\text{.}\) We now consider what happens as we traverse those paths overlayed on \(f\text{.}\) To answer this questions we consider the limits
\begin{equation*}
\lim_{t\to t_0} f(x_1(t), y_1(t)) \qquad \text{and} \qquad \lim_{t\to t_0} f(x_2(t), y_2(t)) \text{.}
\end{equation*}
If these limits are different, then we know our original limit, \(\lim_{(x,y) \to (a,b)} f(x,y) \) does not exists.
Activity 6.4.2.
Consider the function given by
\begin{equation*}
f(x,y) = \frac{xy}{x^2+y^2}
\end{equation*}
and the limit
\begin{equation}
\lim_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2} \text{.}\tag{6.4.2}
\end{equation}
(a)
Is the function continuous at \((0,0)\text{?}\) Explain why or why not?
(b)
Consider the path \(c(t)=(t,0)\text{.}\) Graph this path and confirm that this path goes to \((0,0)\) at \(t \to 0\text{.}\)
(c)
Substitute this path into
\begin{equation*}
\lim_{t\to 0 } f(x(t), y(t))
\end{equation*}
and find the limit.
Hint.
Using the path \(c(t)=(t,0)\) we have \(x(t)=t\) and \(y(t)=0\text{.}\) Thus, the limit becomes
\begin{equation*}
\lim_{t\to 0} f(t,0)\text{.}
\end{equation*}
(d)
(e)
Consider the path \(c(t) = (t , mt)\) were \(m\) is a real number. Graph \(c\) for several values of \(m\text{?}\) What family of functions do these represent?
(f)
Substitute this path into
\begin{equation*}
\lim_{t\to 0 } f(x(t), y(t))
\end{equation*}
and find the limit.
Hint.
Using the path \(c(t)=(t,mt)\) we have \(x(t)=t\) and \(y(t)=mt\text{.}\) Thus, the limit becomes
\begin{equation*}
\lim_{t\to 0} f(t,mt) = \lim_{t\to 0} \frac{mt^2}{t^2 + m^2t^2}\text{.}
\end{equation*}
(g)
Does the limit go to the same value for each value of \(m\text{?}\) What does this tell you about the limit in (6.4.2)?
Activity 6.4.3.
Consider the function given by
\begin{equation*}
f(x,y) = \frac{x^2y}{x^4+y^2}
\end{equation*}
and the limit
\begin{equation}
\lim_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2} \text{.}\tag{6.4.3}
\end{equation}
(a)
Repeat the steps of Activity 6.4.2 for the above limit.
(b)
Consider the path \(c(t) = (t, t^2)\text{.}\) Graph this path and confirm that this path goes to \((0,0)\) at \(t \to 0\text{.}\)
(c)
Substitute this path into
\begin{equation*}
\lim_{t\to 0 } f(x(t), y(t))
\end{equation*}
and find the limit.
Hint.
Using the path \(c(t)=(t,t^2)\) we have \(x(t)=t\) and \(y(t)=t^2\text{.}\) Thus, the limit becomes
\begin{equation*}
\lim_{t\to 0} f(t,t^2)= \lim_{t \to 0} \frac{t^2t^2}{t^4+(t^2)^2}\text{.}
\end{equation*}
(d)
What can we say about the limit in (6.4.3)? Explain.
