Section 8.4 Interactive Playground for Visualizing Vector Fields
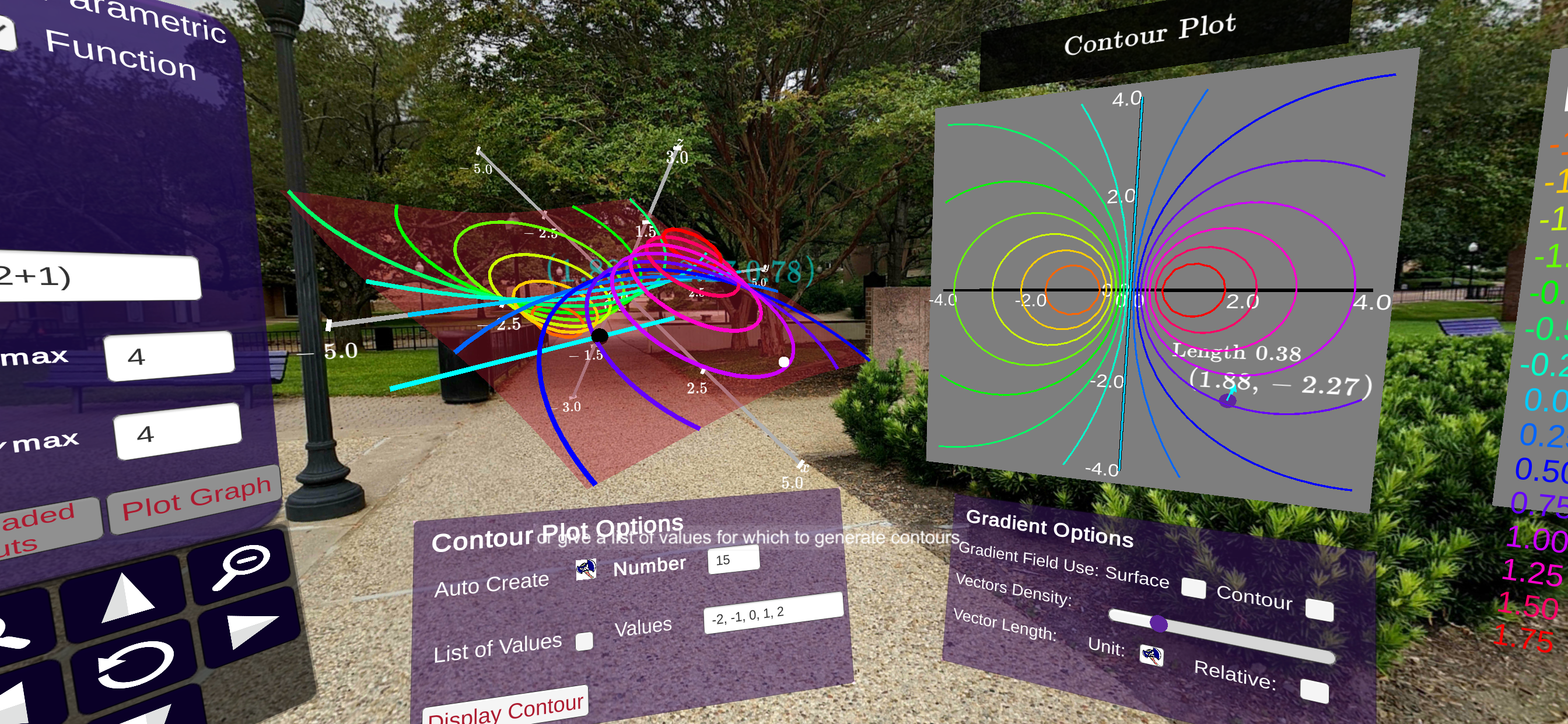
Here we examine the functionality of the Vector Field Playground. This exploratory playground can be used by students to study the vector fields and gradients of multivariable functions and parametric surfaces. The user is able to specify the surface of their choice. Once the surface is graphed level curves are displayed along the curve and the corresponding two dimensional contour plot is displayed.
Here is a list of functionality
Subsection 8.4.1 Entering Vector Field Equations
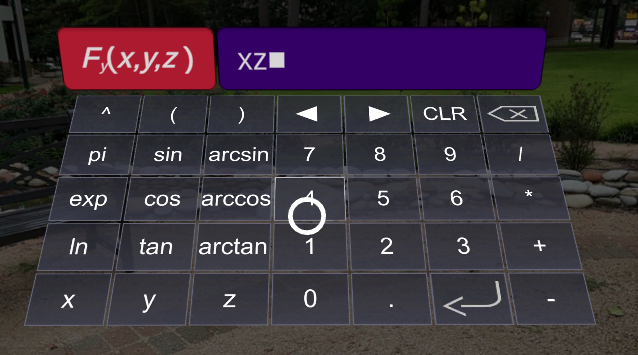
The panel to the left is used to enter equations for the vector fields. These are in the form of \(\mathbf{F}(x,y,z) = \langle F_1(x,y,z), y(u,v), z(u,v) \rangle\text{.}\) When you “click” or “select” one of the textboxes, a keyboard is displayed. This keyboard can be used to enter the equation of your choice. Once you select Enter on the keyboard, the textbox is filled with expression you entered. On the panel clicking or selecting Plot Graph constructs the surface.

Subsection 8.4.2 Loading and Saving Vector Fields
For any set of equations for a vector field, the equations can be saved for later viewing. This is accomplished by selecting Save button on the panel pictured below. You can load the equations you saved (and some equations that are pre-saved) by using the Pre-Loaded Inputs button. Use the arrows to select the equations of choice and click on Display to show the vector field described by the equations.


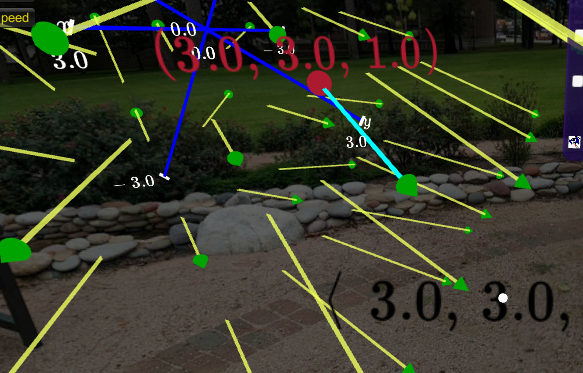
Subsection 8.4.3 Examining Particular Vectors
For the displayed vector field, each vector can be Selected. When the vector is selected, the initial point will be displayed and the value of the vector that the location is also is displayed. An animation displaying the vector will begin.
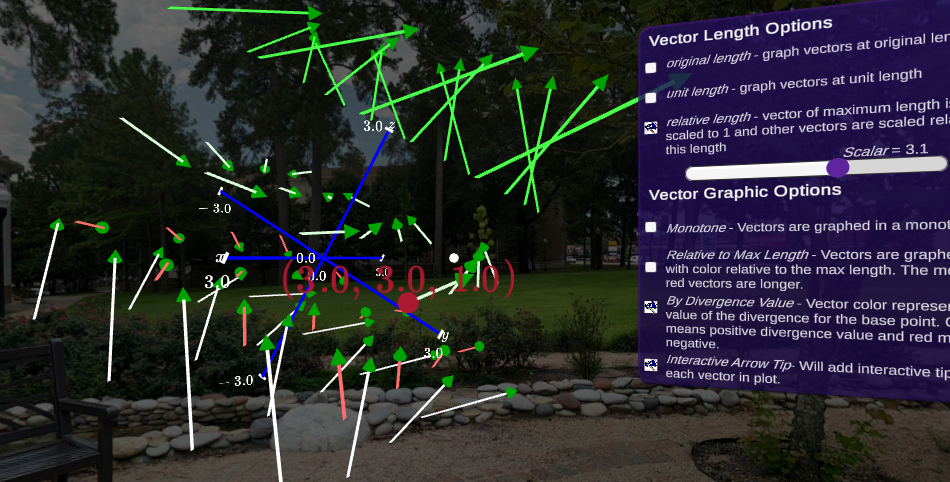
Subsection 8.4.4 Vector Field Display Options
The right hand panel has a myriad of options for displaying the vector field. The default option is that vectors are drawn at their actual length. There are several options for displaying the vectors. An easy thing to do to increase visibility is to use the slider. This will scalar all the vectors using the multiplier on the scale bar.
Length Options.
- original length - all vectors are graphed at their actual length
- unit length - all vectors are normalized to a length of one and graphed
- relative length - the vector with largest magnitude is scaled to a length of one and all other vectors are scaled relative to the maximum vector
Color Options.
- monotone - all vectors are graphed using the same color
- divergence value - vectors are colored based on divergence of the base point. Green vectors have a positive divergence and red vectors mean the base point has a negative divergence.
- relative to max length - vector is colored based on its length with red representing longer vectors and white representing shorter vectors